Elastic Constraints

A constraint $C(x)=c$ (equality may be replaced by $\le$ or $\ge$) can be elasticized to the form

$$C(x)\in D$$

where $D$ denotes some interval containing the value $c$.

Define the constraint in two steps:

1. instantiate constraint (subclass of LpConstraint) with target $c$.

2. call its makeElasticSubProblem() method which returns an object of type FixedElasticSubProblem (subclass of LpProblem) - its objective is the minimization of the distance of $C(x)$ from $D$.

constraint = LpConstraint(..., rhs = c)
elasticProblem = constraint.makeElasticSubProblem(
                       penalty = <penalty_value>,
                       proportionFreeBound = <freebound_value>,
                       proportionFreeBoundList = <freebound_list_value>,
                       )

where:

• <penalty_value> is a real number

• <freebound_value> $a\in [0,1]$ specifies a symmetric target interval $D=(c(1-a),c(1+a))$ about $c$

• <freebound_list_value> = [a,b], a list of proportions $a,b\in [0,1]$ specifying an asymmetric target interval $D=(c(1-a),c(1+b))$ about $c$

The penalty applies to the constraint at points $x$ where $C(x)\notin D$. The magnitude of <penalty_value> can be assessed by examining the final objective function in the .lp file written by LpProblem.writeLP().

Example:

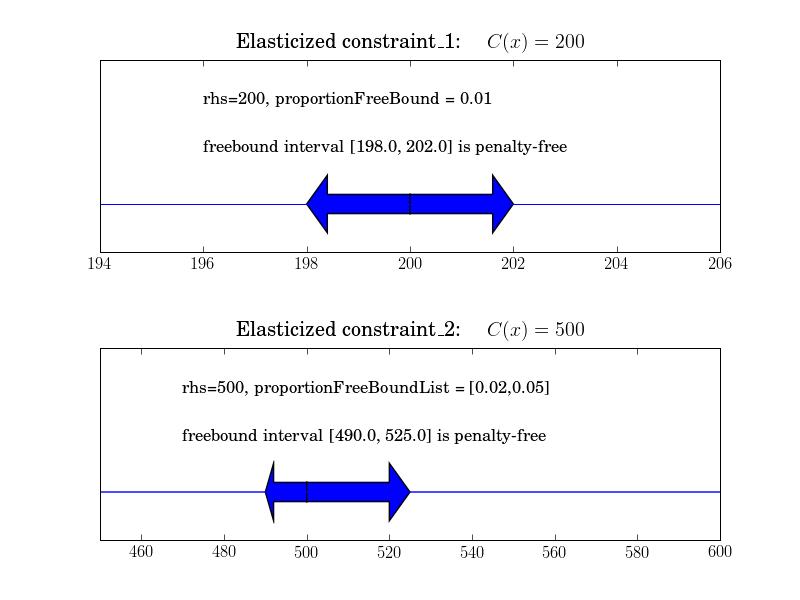
>>> constraint_1 = LpConstraint('ex_1',sense=1,rhs=200)
>>> elasticProblem_1 = constraint_1.makeElasticSubproblem(penalty=1, proportionFreeBound = 0.01)
>>> constraint_2 = LpConstraint('ex_2',sense=0,rhs=500)
>>> elasticProblem_2 = constraint_2.makeElasticSubproblem(penalty=1,
proportionFreeBoundList = [0.02, 0.05])

1. constraint_1 has a penalty-free target interval of 1% either side of the rhs value, 200

2. constraint_2 has a penalty-free target interval of - 2% on left and 5% on the right side of the rhs value, 500

Following are the methods of the return-value: