-
LP_verbosity – integer (0).
- Verbosity level of the LP module.
-
set_obj_upper_lim – boolean (FALSE).
- Whether to stop solving the LP relaxation when it's optimal value is
provably higher than the global upper bound. There are some advantages
to continuing the solution process anyway. For instance, this results
in the highest possible lower bound. On the other hand, if the matrix
is full, this node will be pruned anyway and the rest of the
computation is pointless. This option should be set at FALSE for
column generation since the LP dual values may not be reliable otherwise.
-
try_to_recover_from_error – boolean (TRUE).
- Indicates what should be done in case the LP solver is unable to solve
a particular LP relaxation because of numerical problems. It is
possible to recover from this situation but further results may be
suspect. On the other hand, the entire solution process can be
abandoned.
-
problem_type – integer (ZERO_ONE_PROBLEM{0}).
- The type of problem being solved. Other values are INTEGER_PROBLEM{1} or MIXED_INTEGER_PROBLEM{2}.
(Caution: The mixed-integer option is not well tested.)
-
cut_pool_check_frequency – integer (10).
- The number of iterations between sending LP solutions to the cut pool
to find violated cuts. It is not advisable to check the cut pool too
frequently as the cut pool module can get bogged down and the LP
solution generally do not change that drastically from one iteration
to the next anyway.
-
not_fixed_storage_size – integer (2048).
- The not fixed list is a partial list of indices of variables not
in the matrix that have not been fixed by reduced cost. Keeping this
list allows SYMPHONY to avoid repricing variables (an expensive operation)
that are not in the matrix because they have already been permanently
fixed. When this array reaches its maximum size, no more variable
indices can be stored. It is therefore advisable to keep the maximum
size of this array as large as possible, given memory limitations.
-
max_non_dual_feas_to_add_min,
-
-
max_non_dual_feas_to_add_max,
-
-
max_non_dual_feas_to_add_frac
– integer, integer, double (20, 200, .05).
- These three parameters determine the maximum number of
non-dual-feasible columns that can be added in any one iteration
after pricing. This maximum is set to the indicated
fraction of the current number of active columns unless this numbers
exceeds the given maximum or is less than the given minimum, in which
case, it is set to the max or min, respectively.
-
max_not_fixable_to_add_min,
-
-
max_not_fixable_to_add_max,
-
-
max_not_fixable_to_add_frac – integer, integer, double (100,
500, .1)
- As above, these three parameters determine the maximum number of new
columns to be added to the problem because they cannot be priced out.
These variables are only added when trying to restore infeasibility
and usually, this does not require many variables anyway.
-
mat_col_compress_num, mat_col_compress_ratio – integer,
double (50, .05).
- Determines when the matrix should be physically compressed. This only
happens when the number of columns is high enough to make it
“worthwhile.” The matrix is physically compressed when the number of
deleted columns exceeds either an absolute number and a specified
fraction of the current number of active columns.
-
mat_row_compress_num, mat_row_compress_ratio – integer,
double (20, .05).
- Same as above except for rows.
-
tailoff_gap_backsteps, tailoff_gap_frac – integer, double
(2, .99).
- Determines when tailoff is detected in the LP module.
Tailoff is reported if the average ratio of the current gap to the
previous iteration's gap over the last
tailoff_gap_backsteps
iterations wasn't at least
tailoff_gap_frac.
-
tailoff_obj_backsteps, tailoff_obj_frac – integer, double
(2, .99).
- Same as above, only the ratio is taken with respect to the change in
objective function values instead of the change in the gap.
-
ineff_cnt_to_delete – integer (0).
- Determines after how many iterations of being deemed ineffective a
constraint is removed from the current relaxation.
-
eff_cnt_before_cutpool – integer (3).
- Determines after how many iterations of being deemed effective each
cut will be sent to the global pool.
-
ineffective_constraints – integer
(BASIC_SLACKS_ARE_INEFFECTIVE{2}).
- Determines under what condition a constraint is deemed ineffective in
the current relaxation. Other possible values are NO_CONSTRAINT_IS_INEFFECTIVE{0}, NONZERO_SLACKS_ARE_INEFFECTIVE{1}, and
ZERO_DUAL_VALUES_ARE_INEFFECTIVE{3}.
-
base_constraints_always_effective – boolean (TRUE).
- Determines whether the base constraints can ever be removed from the
relaxation. In some case, removing the base constraints from the
problem can be disastrous depending on the assumptions made by the cut
generator.
-
branch_on_cuts – boolean (FALSE).
- This informs the framework whether the user plans on branching on cuts
or not. If so, there is additional bookkeeping to be done, such as
maintaining a pool of slack cuts to be used for branching. Therefore,
the user should not set this flag unless he actually plans on using
this feature.
-
discard_slack_cuts – integer (DISCARD_SLACKS_BEFORE_NEW_ITERATION{0}).
- Determines when the pool of slack cuts is discarded. The other option
is DISCARD_SLACKS_WHEN_STARTING_NEW_NODE{1}.
-
first_lp_first_cut_time_out,
-
-
first_lp_all_cuts_time_out,
-
-
later_lp_first_cut_time_out,
-
-
later_lp_all_cuts_time_out –
double (0, 0, 5, 1).
- The next group of parameters determines when the LP should give up
waiting for cuts from the cut generator and start to solve the
relaxation in its current form or possibly branch if necessary. There
are two factors that contribute to determining this timeout. First
is whether this is the first LP in the search node of whether it is a
later LP. Second is whether any cuts have been added already in this
iteration. The four timeout parameters correspond to the four possible
combinations of these two variables.
-
no_cut_timeout –
- This keyword does not have an associated value. If this keyword
appears on a line by itself or with a value, this tells the framework
not to time out while waiting for cuts. This is useful for debugging
since it enables runs with a single LP module to be duplicated.
-
all_cut_timeout – double (no default).
- This keyword tells the framework to set all of the above timeout
parameters to the value indicated.
-
max_cut_num_per_iter – integer (20).
- The maximum number of cuts that can be added to the LP in an
iteration. The remaining cuts stay in the local pool to be added in
subsequent iterations, if they are strong enough.
-
do_reduced_cost_fixing – boolean (FALSE).
- Whether or not to attempt to fix variables by reduced cost. This
option is highly recommended
-
gap_as_ub_frac, gap_as_last_gap_frac – double (.1, .7).
- Determines when reduced cost fixing should be attempted. It is only
done when the gap is within the fraction
gap_as_ub_frac of the upper
bound or when the gap has decreased by the fraction
gap_as_last_gap_frac since the last time variables were fixed.
-
do_logical_fixing – boolean (FALSE).
- Determines whether the user's logical fixing routine should be used.
-
fixed_to_ub_before_logical_fixing,
-
-
fixed_to_ub_frac_before_logical_fixing –
integer, double (1, .01).
- Determines when logical fixing should be attempted. It will be called
only when a certain absolute number and a certain number of variables
have been fixed to their upper bounds by reduced cost. This is because
it is typically only after fixing variables to their upper bound that
other variables can be logically fixed.
-
max_presolve_iter – integer (10).
- Number of simplex iterations to be performed in the pre-solve for
strong branching.
-
strong_branching_cand_num_max,
-
-
strong_branching_cand_num_min,
-
-
strong_branching_red_ratio –
integer (10, 5, 1).
- These three parameters together determine the number of strong
branching candidates to be used by default. In the root node,
strong_branching_cand_num_max candidates are used. On each
succeeding level, this number is reduced by the number
strong_branching_red_ratio multiplied by the square of the level.
This continues until the number of candidates is reduced to
strong_branching_cand_num_min and then that number of candidates
is used in all lower levels of the tree.
-
strong_branching_high_low_weight – double (0.8).
- This parameter is used to calculate the score of each branching candidate. The
candidate with the highest score is then selected for branching. Let
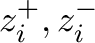 be the estimated change in objective function value when we branch on
the candidate
be the estimated change in objective function value when we branch on
the candidate  . Then the score of candidate
. Then the score of candidate  is
is
 , where
, where
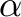 is the value of
strong_branching_high_low_weight. This
value should always lie in the interval
is the value of
strong_branching_high_low_weight. This
value should always lie in the interval ![$[0,1]$](img65.png) .
.
-
limit_strong_branching_time
- – boolean (TRUE).]
Whether to heuristically limit the amount of time spent in strong branching.
-
use_hot_starts – boolean (TRUE).
- Determines if the LP solver is asked to make special arrangements for doing
dual-simplex iterations when bounds on a variable are changed for strong
branching. Some LP solvers provide such options so that strong branching can
be performed much faster than the regular dual-simplex procedure.
-
should_use_rel_br – boolean (TRUE).
- Determines if reliability braching is used to determine branching candidates
or not. This parameter is set to FALSE if OPENMP is used. When this
branching rule is disabled, strong branching is used to select a candidate.
-
rel_br_override_default – boolean (TRUE).
- If reliability branching is enabled and this paramter is set to TRUE then the
policy of selecting branching candidates is automatically adjusted on the
basis of bounds on solution value and the time elapsed. If this parameter is
set to FALSE, the policy is based on the values of the following three
parameters.
-
rel_br_threshold – integer (8).
- It is assumed that the score obtained by branching on a given variable these many
times is reliable for estimating the pseudocosts of this variable in the rest
of the branch-and-bound algorithm. In other words, if reliability branching is
enabled, strong branching is used on a variable at most
rel_br_threshold many times.
-
rel_br_max_solves – integer (20).
- If reliability branching is enabled, this parameter determines the maximum
number of strong branching LPs that are solved in each node. If some branching
candidates have reliable estimates, the number of LPs can be less than
the value of this parameter.
-
rel_br_cand_threshold – integer (10).
- If reliability branching is enabled, then strong branching is stopped if the
last
rel_br_cand_threshold LPs did not give a better improvement in
the lower bound.
-
is_feasible_default – integer (TEST_INTEGRALITY{1}).
- Determines the default test to be used to determine feasibility. This
parameter is provided so that the user can change the default behavior
without recompiling. The only other option is TEST_ZERO_ONE{0}.
-
send_feasible_solution_default – integer
(SEND_NONZEROS{0}).
- Determines the form in which to send the feasible solution. This
parameter is provided so that the user can change the default behavior
without recompiling. This is currently the only option.
-
send_lp_solution_default – integer (SEND_NONZEROS{0}).
- Determines the default form in which to send the LP solution to the
cut generator and cut pool. This
parameter is provided so that the user can change the default behavior
without recompiling. The other option is SEND_FRACTIONS{1}.
-
display_solution_default – integer (DISP_NOTHING{0}).
- Determines how to display the current LP solution if desired.
See the description of user_display_solution() for other
possible values. This parameter is provided so that
the user can change the default behavior without recompiling.
-
shall_we_branch_default – integer
(USER__BRANCH_IF_MUST{2}).
- Determines the default branching behavior. Other values are USER__DO_NOT_BRANCH{0} (not recommended as a default), USER__DO_BRANCH{1} (also not recommended as a default), and USER__BRANCH_IF_TAILOFF{3}. This
parameter is provided so that the user can change the default behavior
without recompiling.
-
select_candidates_default – integer (USER__CLOSE_TO_HALF_AND_EXPENSIVE{10}).
- Determines the default rule for selecting strong branching candidates.
Other values are USER__CLOSE_TO_HALF{10} and
USER__CLOSE_TO_ONE_AND_CHEAP{12}. This
parameter is provided so that the user can change the default behavior
without recompiling.
-
compare_candidates_default – integer
(HIGHEST_LOW_OBJ{2}).
- Determines the default rule for comparing candidates. See the
description of user_compare_candidates() for other values. This
parameter is provided so that the user can change the default behavior
without recompiling.
-
select_child_default – integer
(PREFER_LOWER_OBJ_VALUE{0}).
- Determines the default rule for selecting the child to be processed
next. For other possible values, see the description
user_select_child(). This
parameter is provided so that the user can change the default behavior
without recompiling.
-
mc_find_supported_solutions – boolean (FALSE).
- By default, sym_mc_solve routine will find all the non-dominated
solutions if the problem to be solved is
a bicriteria problem. However, if the user plans to find only the supported
solutions, then, this parameter has to be set before
calling sym_mc_solve routine.
-
mc_rho – double (0.00001).
- The value used in augmented Chebyshev norm during the bicriteria
solution procedure.
-
generate_cgl_cuts – boolean (TRUE).
- Whether or not to generate cuts using COIN's cut generation library.
Note that, to use CGL cuts, OSI interface has to be used and moreover the
corresponding flags have to be set during installation. See the makefile for
more details.
-
generate_cgl_gomory_cuts – integer (GENERATE_DEFAULT).
-
-
generate_cgl_knapsack_cuts – integer (GENERATE_DEFAULT).
-
-
generate_cgl_twomir_cuts – integer (GENERATE_ONLY_IN_ROOT).
-
-
generate_cgl_clique_cuts – integer (GENERATE_DEFAULT).
-
-
generate_cgl_oddhole_cuts – integer (DO_NOT_GENERATE).
-
-
generate_cgl_flowcover_cuts – integer (GENERATE_DEFAULT).
-
This set of parameters is for controlling when certain classes of cuts are to
be generated. It can take on the values enumerated below (see values
in symphony.h).
- DO_NOT_GENERATE (-1): Do not generate cuts of this class.
- GENERATE_DEFAULT (0): Use SYMPHONY's automatic tuning for generation of
this class of cuts.
- GENERATE_IF_IN_ROOT (1): Generate these cuts in the tree only if at
least one violated cut is generated in the root node.
- GENERATE_ONLY_IN_ROOT (2): Generate these cuts only in the root node.
- GENERATE_ALWAYS (3): Generate these cuts every time cut generation is
done.
- GENERATE_PERIODICALLY (4): Generate these cuts every
 time the cut generator is called, where
time the cut generator is called, where 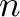 is set by the parameter
generate_cgl_xxx_cuts_freq.
is set by the parameter
generate_cgl_xxx_cuts_freq.
See https://projects.coin-or.org/Cgl for a description of these
classes and others that could be added.
-
generate_cgl_gomory_cuts_freq – integer (5).
-
-
generate_cgl_knapsack_cuts_freq – integer (5).
-
-
generate_cgl_twomir_cuts_freq – integer (5).
-
-
generate_cgl_clique_cuts_freq – integer (5).
-
-
generate_cgl_oddhole_cuts_freq – integer (5).
-
-
generate_cgl_flowcover_cuts_freq – integer (5).
-
The frequency with which to generate cuts if the
parameter cgl_generate_xxx_cuts for the
corresponding class is set to GENERATE_PERIODICALLY.
-
fp_enabled – integer (SYM_FEAS_PUMP_DEFAULT{1}).
- Determines the overall policy of using the feasibility pump heuristic to find
feasible solutions. SYM_FEAS_PUMP_DEFAULT{1} indicates that the
decision to use the heuristic is determined on the basis of current values of
lower bound, upper bound, the time used etc., based on some preset rules. SYM_FEAS_PUMP_REPEATED{2} indicates that the heuristic will be used
every few iterations until the problem is solved. The frequency can be
adjusted through the
fp_frequency parameter. SYM_FEAS_PUMP_TILL_SOL{3} indicates that the heuristic is used only
until the first feasible solution is found. SYM_FEAS_PUMP_DISABLE{-1} indicates that the heuristic is not used.
-
fp_frequency – integer (10).
- Determines the number of LPs that are solved before which the feasibility pump
heuristic is called again. This parameter is used only if the parameter
fp_enabled is set to SYM_FEAS_PUMP_REPEATED{2}. Otherwise,
the frequency is determined automatically based on some preset rules.
-
fp_max_cycles – integer (100).
- Determines the maximum number of LPs that can be solved in a call to the
feasibility pump heuristic. A higher number might be helpful in finding a
better feasible solution but may result in more time spent in the heuristic.
-
fp_time_limit – double (50).
- If a feasible solution has been found, this parameter determines the time in
seconds that can be spent on the feasibility pump heuristic. If a solution has
not been found yet, the parameter
fp_max_initial_time is used.
-
fp_max_initial_time – double (100).
- If a feasible solution has not been found, this parameter determines the time in
seconds that can be spent on the feasibility pump heuristic. If a solution has
been found, the parameter
fp_time_limit is used.
-
fp_min_gap – double (0.5).
- If the relative (%) gap between the lower and the upper bounds falls below the
value of this parameter, feasibility pump is not called.
-
fp_flip_fraction – double (0.1).
- When the feasibility pump gets stuck in a cycle, this fraction of binary
variables are flipped. The variables are selected randomly. Increasing the
value of this parameter may result in the pump getting stuck fewer number of
times, but the time to solve LPs after flipping may increase substantially.
-
fp_poor_sol_lim_fac – integer (10).
- Sometimes the feasibility pump keeps generating solutions that have high
objective function values. When the number of such solutions becomes more than
fp_poor_sol_lim_fac times the number of “good” solutions, the pump
is disabled.
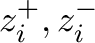 be the estimated change in objective function value when we branch on
the candidate
be the estimated change in objective function value when we branch on
the candidate  . Then the score of candidate
. Then the score of candidate  is
is
 , where
, where
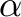 is the value of
strong_branching_high_low_weight. This
value should always lie in the interval
is the value of
strong_branching_high_low_weight. This
value should always lie in the interval ![$[0,1]$](img65.png) .
.
 time the cut generator is called, where
time the cut generator is called, where 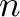 is set by the parameter
generate_cgl_xxx_cuts_freq.
is set by the parameter
generate_cgl_xxx_cuts_freq.