A Sudoku Problem formulated as an LP
Problem Description
A sudoku problem is a problem with an incomplete 9x9 table of numbers that must be filled according to several rules:
Within any of the 9 individual 3x3 boxes, each of the numbers 1 to 9 must be found.
Within any column of the 9x9 grid, each of the numbers 1 to 9 must be found.
Within any row of the 9x9 grid, each of the numbers 1 to 9 must be found.
On this page we will formulate the problem below (from wikipedia) as a model using PuLP. Once created, our code will need little modification to solve any sudoku problem.
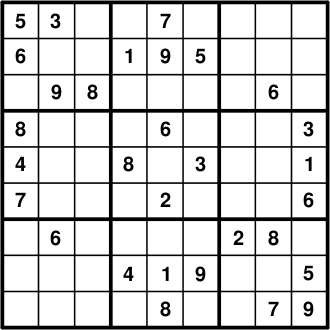
Formulation
Identify the Decision Variables
In order to formulate this problem as a linear program, we could simply create a variable for each of the 81 squares between 1 and 9 representing the value in that square. However, this is awfully complicated because in linear programming there is no “not equal to” operator and so we cannot use the necessary constraints of no squares within a box/row/column being equal in value to each other. Whilst we can ensure the sum of all the values in a box/row/column equal 45, this will still result in many solutions satisfying the 45 constraint but still with 2 of the same number in the same box/row/column. There is a solution for this using Big M constraints that compare for each pair of values in a box/column/row which number is strictly smaller than the other but we prefer to present an approach that is much more elegant:
We create 729 individual binary (0-1) problem variables. These represent 9 problem variables per square for each of 81 squares, where the 9 variables each correspond to the number that might be in that square. The binary nature of the variable says whether the existence of that number in that square is true or false. Therefore, there can clearly be only 1 of the 9 variables for each square as true (1) and the other 8 must be false (0) since only one number can be placed into any square. This will become clear below.
Formulate the Objective Function
Interestingly, with sudoku there is no solution that is better than another
solution, since a solution by definition must satisfy all the constraints.
Therefore, we are not really trying to minimise or maximise anything, we are
just trying to find the values on our variables that satisfy the constraints.
Thus, we neither set LpMinimize or LpMaximize nor define an objective function.
Formulate the Constraints
These are simply the known constraints of a sudoku problem plus the constraints on our own created variables we have used to express the features of the problem:
The values in the squares in any row must be each of 1 to 9.
The values in the squares in any column must be each of 1 to 9.
The values in the squares in any box must be each of 1 to 9. (a box is one of the 9 non-overlapping 3x3 grids within the overall 9x9 grid)
There must be only one number within any square (seems logically obvious, but it is important to our formulation to ensure because of our variable choices).
The starting sudoku numbers must be in those same places in the final solution (this is a constraint since these numbers are not changeable in the actual problem, whereas we can control any other numbers. If none or very few starting numbers were present, the sudoku problem would have a very large number of feasible solutions, instead of just one).
Solution
The introductory commenting and import statement are entered
"""
The Sudoku Problem Formulation for the PuLP Modeller
Authors: Antony Phillips, Dr Stuart Mitchell
edited by Nathan Sudermann-Merx
"""
# Import PuLP modeler functions
from pulp import *
In the unique case of the sudoku problem, the row names, column names and variable option values are all the exact same list of numbers from 1 to 9.
# All rows, columns and values within a Sudoku take values from 1 to 9
VALS = ROWS = COLS = range(1, 10)
A list called Boxes is created with 9 elements, each being another list. These 9 lists correspond to each of the 9 boxes, and each of the lists contains tuples as the elements with the row and column indices for each square in that box. Explicitly entering the values in a similar way to the following would have had the same effect (but would have been a waste of time):
# The boxes list is created, with the row and column index of each square in each box
Boxes = [
[(3 * i + k + 1, 3 * j + l + 1) for k in range(3) for l in range(3)]
for i in range(3)
for j in range(3)
]
Therefore, Boxes[0] will return a list of tuples containing the locations of each of the 9 squares in the first box.
The prob variable is created to contain the problem data.
# The prob variable is created to contain the problem data
prob = LpProblem("Sudoku Problem")
The 729 problem variables are created since the (Vals,Rows,Cols) creates a variable for each combination of value, row and column. An example variable would be: Choice_4_2_9, and it is defined to be a binary variable (able to take only the integers 1 or 0. If Choice_4_2_9 was 1, it would mean the number 4 was present in the square situated in row 2, column 9. (If it was 0, it would mean there was not a 4 there)
# The decision variables are created
choices = LpVariable.dicts("Choice", (VALS, ROWS, COLS), cat="Binary")
As explained above, we don’t define an objective function since we are only concerned with any variable combination that can satisfy the constraints.
# We do not define an objective function since none is needed
Since there are 9 variables for each square, it is important to specify that only exactly one of them can take the value of 1 (and the rest are 0). Therefore, the below code reads: for each of the 81 squares, the sum of all the 9 variables (each representing a value that could be there) relating to that particular square must equal 1.
# A constraint ensuring that only one value can be in each square is created
for r in ROWS:
for c in COLS:
prob += lpSum([choices[v][r][c] for v in VALS]) == 1
These constraints ensure that each number (value) can only occur once in each row, column and box.
# The row, column and box constraints are added for each value
for v in VALS:
for r in ROWS:
prob += lpSum([choices[v][r][c] for c in COLS]) == 1
for c in COLS:
prob += lpSum([choices[v][r][c] for r in ROWS]) == 1
for b in Boxes:
prob += lpSum([choices[v][r][c] for (r, c) in b]) == 1
The starting numbers are entered as constraints i.e a 5 in row 1 column 1 is true.
# The starting numbers are entered as constraints
input_data = [
(5, 1, 1),
(6, 2, 1),
(8, 4, 1),
(4, 5, 1),
(7, 6, 1),
(3, 1, 2),
(9, 3, 2),
(6, 7, 2),
(8, 3, 3),
(1, 2, 4),
(8, 5, 4),
(4, 8, 4),
(7, 1, 5),
(9, 2, 5),
(6, 4, 5),
(2, 6, 5),
(1, 8, 5),
(8, 9, 5),
(5, 2, 6),
(3, 5, 6),
(9, 8, 6),
(2, 7, 7),
(6, 3, 8),
(8, 7, 8),
(7, 9, 8),
(3, 4, 9),
(1, 5, 9),
(6, 6, 9),
(5, 8, 9),
]
for v, r, c in input_data:
prob += choices[v][r][c] == 1
The problem is written to an LP file, solved using PuLP’s choice of solver and the solution status is printed to the screen
# The problem data is written to an .lp file
prob.writeLP("Sudoku.lp")
# The problem is solved using PuLP's choice of Solver
prob.solve()
# The status of the solution is printed to the screen
print("Status:", LpStatus[prob.status])
Instead of printing out all 729 of the binary problem variables and their respective values, it is more meaningful to draw the solution in a text file. The code also puts lines inbetween every third row and column to make the solution easier to read. The sudokuout.txt file is created in the same folder as the .py file.
# A file called sudokuout.txt is created/overwritten for writing to
sudokuout = open("sudokuout.txt", "w")
# The solution is written to the sudokuout.txt file
for r in ROWS:
if r in [1, 4, 7]:
sudokuout.write("+-------+-------+-------+\n")
for c in COLS:
for v in VALS:
if value(choices[v][r][c]) == 1:
if c in [1, 4, 7]:
sudokuout.write("| ")
sudokuout.write(str(v) + " ")
if c == 9:
sudokuout.write("|\n")
sudokuout.write("+-------+-------+-------+")
sudokuout.close()
A note of the location of the solution is printed to the solution
# The location of the solution is give to the user
print("Solution Written to sudokuout.txt")
The full file above is given provided Sudoku1.py
The final solution should be the following:
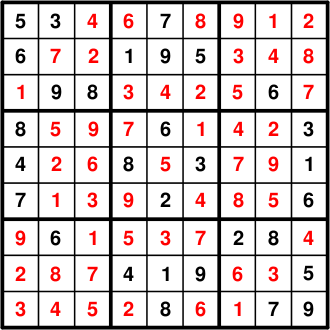
Extra for Experts
In the above formulation we did not consider the fact that there may be multiple solutions if the sudoku problem is not well defined.
We can make our code return all the solutions by editing our code as shown after the prob.writeLP line. Essentially we are just looping over the solve statement, and each time after a successful solve, adding a constraint that the same solution cannot be used again. When there are no more solutions, our program ends.
while True:
prob.solve()
# The status of the solution is printed to the screen
print("Status:", LpStatus[prob.status])
# The solution is printed if it was deemed "optimal" i.e met the constraints
if LpStatus[prob.status] == "Optimal":
# The solution is written to the sudokuout.txt file
for r in ROWS:
if r in [1, 4, 7]:
sudokuout.write("+-------+-------+-------+\n")
for c in COLS:
for v in VALS:
if value(choices[v][r][c]) == 1:
if c in [1, 4, 7]:
sudokuout.write("| ")
sudokuout.write(str(v) + " ")
if c == 9:
sudokuout.write("|\n")
sudokuout.write("+-------+-------+-------+\n\n")
# The constraint is added that the same solution cannot be returned again
prob += (
lpSum(
[
choices[v][r][c]
for v in VALS
for r in ROWS
for c in COLS
if value(choices[v][r][c]) == 1
]
)
<= 80
)
# If a new optimal solution cannot be found, we end the program
else:
break
sudokuout.close()
The full file using this is available Sudoku2.py. When using this code for sudoku problems with a large number of solutions, it could take a very long time to solve them all. To create sudoku problems with multiple solutions from unique solution sudoku problem, you can simply delete a starting number constraint. You may find that deleting several constraints will still lead to a single optimal solution but the removal of one particular constraint leads to a sudden dramatic increase in the number of solutions.