Next: The Node Processing Module Up: The Master Module Previous: Modifying Problem Data. Contents
For those readers not familiar with bicriteria integer programming, we briefly review the basic notions here. For clarity, we restrict the discussion here to pure integer programs (ILPs), but the principles are easily generalized. A bicriteria ILP is a generalization of a standard ILP presented earlier that includes a second objective function, yielding an optimization problem of the form
The operator vmin is understood to mean that solving this program is the problem of generating efficient solutions, which are these feasible solutions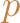 to 4.2 for which there does not exist a second
distinct feasible solution
to 4.2 for which there does not exist a second
distinct feasible solution
 such that
such that
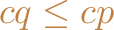 and
and
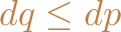 and at
least one inequality is strict. Note that (4.2) does not have a
unique optimal solution value, but a set of pairs of solution values called
outcomes. The pairs of solution values corresponding to efficient
solutions are called Pareto outcomes. Surveys of methodology for for
enumerating the Pareto outcomes of multicriteria integer programs are provided
by Climaco et al. [7] and more recently by Ehrgott and
Gandibleux [11,12] and Ehrgott and
Wiecek [13].
and at
least one inequality is strict. Note that (4.2) does not have a
unique optimal solution value, but a set of pairs of solution values called
outcomes. The pairs of solution values corresponding to efficient
solutions are called Pareto outcomes. Surveys of methodology for for
enumerating the Pareto outcomes of multicriteria integer programs are provided
by Climaco et al. [7] and more recently by Ehrgott and
Gandibleux [11,12] and Ehrgott and
Wiecek [13].
The bicriteria ILP (4.2) can be converted to a standard ILP by
taking a nonnegative linear combination of the objective
functions [17]. Without loss of generality, the weights can be
scaled so they sum to one, resulting in a family of ILPs parameterized by a
scalar
 , with the bicriteria objective function replaced
by the weighted sum objective
, with the bicriteria objective function replaced
by the weighted sum objective
 produces a different single-objective
problem. Solving the resulting ILP produces a Pareto outcome called a
supported outcome, since it is an extreme point on the convex lower
envelope of the set of Pareto outcomes. Unfortunately, not all efficient
outcomes are supported, so it is not possible to enumerate the set of Pareto
outcomes by solving a sequence of ILPs from this parameterized family. To
obtain all Pareto outcomes, one must replace the weighted sum objective
(4.3) with an objective based on the weighted Chebyshev norm
studied by Eswaran et al. [14] and Solanki [34]. If
produces a different single-objective
problem. Solving the resulting ILP produces a Pareto outcome called a
supported outcome, since it is an extreme point on the convex lower
envelope of the set of Pareto outcomes. Unfortunately, not all efficient
outcomes are supported, so it is not possible to enumerate the set of Pareto
outcomes by solving a sequence of ILPs from this parameterized family. To
obtain all Pareto outcomes, one must replace the weighted sum objective
(4.3) with an objective based on the weighted Chebyshev norm
studied by Eswaran et al. [14] and Solanki [34]. If
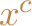 is a solution to a weighted sum problem with
is a solution to a weighted sum problem with
 and
and
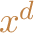 is
the solution with
is
the solution with
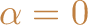 , then the weighted Chebyshev norm of a feasible
solution
, then the weighted Chebyshev norm of a feasible
solution
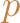 is
Although this objective function is not linear, it can easily be linearized by
adding an artificial variable, resulting in a second parameterized family of
ILPs. Under the assumption of uniform dominance, Bowman showed that an
outcome is Pareto if and only if it can be obtained by solving some ILP in
this family [5]. In [31], the authors presented a method for
enumerating all Pareto outcomes by solving a sequence of ILPs in this
parameterized family. By slightly perturbing the objective function, they also
showed how to relax the uniform dominance assumption. Note that the set of all
supported outcomes, which can be thought of as an approximation of the set of
Pareto outcomes, can be similarly obtained by solving a sequence of ILPs with
weighted sum objectives.
is
Although this objective function is not linear, it can easily be linearized by
adding an artificial variable, resulting in a second parameterized family of
ILPs. Under the assumption of uniform dominance, Bowman showed that an
outcome is Pareto if and only if it can be obtained by solving some ILP in
this family [5]. In [31], the authors presented a method for
enumerating all Pareto outcomes by solving a sequence of ILPs in this
parameterized family. By slightly perturbing the objective function, they also
showed how to relax the uniform dominance assumption. Note that the set of all
supported outcomes, which can be thought of as an approximation of the set of
Pareto outcomes, can be similarly obtained by solving a sequence of ILPs with
weighted sum objectives.
SYMPHONY 5.7.1 contains a generic implementation of the algorithm described in [31], along with a number of methods for approximating the set of Pareto outcomes. To support these capabilities, we have extended the OSI interface so that it allows the user to define a second objective function. Of course, we have also added a method for invoking this bicriteria solver called multiCriteriaBranchAndBound(). Relaxing the uniform dominance requirement requires the underlying ILP solver to have the ability to generate, among all optimal solutions to a ILP with a primary objective, a solution minimizing a given secondary objective. We added this capability to SYMPHONY through the use of optimality cuts, as described in [31].
Because implementing the algorithm requires the solution of a sequence of ILPs that vary only in their objective functions, it is possible to use warm starting to our advantage. Although the linearization of (4.4) requires modifying the constraint matrix from iteration to iteration, it is easy to show that these modifications cannot invalidate the basis. In the case of enumerating all supported outcomes, only the objective function is modified from one iteration to the next. In both cases, we save warm start information from the solution of the first ILP in the sequence and use it for each subsequent computation.