Next: cut_data Up: LP module callbacks Previous: MIPdesc Contents
One of the few internally defined data structures that the user has to deal
with frequently is the MIPdesc data structure, which holds the data
needed to describe a MILP. This data structure is used by SYMPHONY for two
purposes. First, it is used to store the description of a generic MILP that is
either read in from an MPS or AMPL file. More importantly, it is the data
structure the user must use to pass the subproblem descriptions back to
SYMPHONY at the time a new search tree node is created in the function
user_create_subproblem(). The structure has 14 fields (listed
below) that must be filled out to describe a subproblem (some fields are
optional).
A subproblem is a mixed-integer program defined by a matrix of constraints, an
objective function, bounds on both the right hand side values of the
constraints and the variables, an array indicating which variables are
integer, and (optionally) an array of column names that allows SYMPHONY to
report the solution back in terms of column names instead of user indices. If
the subproblem has n variables and m constraints, the
constraints are given by a constraint coefficient matrix of size m
 n (described in the next paragraph). The sense of each
constraint, the right hand side values and bounds on the right hand side
(called range) are vectors are of size m. The objective
function coefficients and the lower and upper bounds on the variables are
vectors of length n. The sense of each constraint can be either 'L'
(
n (described in the next paragraph). The sense of each
constraint, the right hand side values and bounds on the right hand side
(called range) are vectors are of size m. The objective
function coefficients and the lower and upper bounds on the variables are
vectors of length n. The sense of each constraint can be either 'L'
(
 ), 'E' (
), 'E' (
 ), 'G' (
), 'G' (
 ) or 'R' (ranged). For non-ranged rows the
range value is 0, for a ranged row the range value must be non-negative
and the constraint means that the row activity level has to be between the
right hand side value and the right hand side increased by the range value.
) or 'R' (ranged). For non-ranged rows the
range value is 0, for a ranged row the range value must be non-negative
and the constraint means that the row activity level has to be between the
right hand side value and the right hand side increased by the range value.
Since the coefficient matrix is very often sparse, only the nonzero entries
are stored. Each entry of the matrix has a column index, a row index and a
coefficient value associated with it. A matrix is specified in the form of the
three arrays matval, matind, and matbeg. The array
matval contains the values of the nonzero entries of the matrix in
column order; that is, all the entries for the
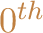 column come
first, then the entries for the
column come
first, then the entries for the
 column, etc. The row index
corresponding to each entry of matval is listed in matind
(both of them are of length nz, the number of nonzero entries in the
matrix). Finally,
matbeg contains the starting positions of each of the columns in
matval and matind. Thus, matbeg[i] is the position
of the first entry of column i in both matval and
matind). By convention matbeg is allocated to be of length
n+1, with matbeg[n] containing the position after the very
last entry in matval and matind (so it is very conveniently
equal to nz). This representation of a matrix is known as a column ordered or column major representation. Below are listed the
fields that must be filled out to describe a subproblem.
column, etc. The row index
corresponding to each entry of matval is listed in matind
(both of them are of length nz, the number of nonzero entries in the
matrix). Finally,
matbeg contains the starting positions of each of the columns in
matval and matind. Thus, matbeg[i] is the position
of the first entry of column i in both matval and
matind). By convention matbeg is allocated to be of length
n+1, with matbeg[n] containing the position after the very
last entry in matval and matind (so it is very conveniently
equal to nz). This representation of a matrix is known as a column ordered or column major representation. Below are listed the
fields that must be filled out to describe a subproblem.