Next: Reference Up: Developing Custom Applications Previous: Other Debugging Techniques Contents
This section was contributed by Michael Trick a few years ago and is a walkthrough of the steps for developing a very simple application using SYMPHONY. Rather than presenting the code in its final version, we will go through the steps that a user would go through. Note that some of the code is lifted from the vehicle routing application. This code is designed to be a sequential code. The MATCH application discussed here is part of the SYMPHONY distribution and the source code can be found in the SYMPHONY/Applications/MATCH directory.
The goal is to create a minimum matching on a complete graph. Initially, we will just formulate this as an integer program with one variable for each possible pair that can be matched. Then we will include a set of constraints that can be added by cut generation.
We begin with the template code in the USER subdirectory included with SYMPHONY. This gives stubs for each user callback routine. First, I need to define a data structure for describing an instance of the matching problem. We use the template structure USER_PROBLEM in the file include/user.h for this purpose. To describe an instance, we just need the number of nodes and the cost matrix. In addition, we also need a way of assigning an index to each possible assignment. Here is the data structure:
typedef struct USER_PROBLEM{
int numnodes;
int cost[MAXNODES][MAXNODES];
int match1[MAXNODES*(MAXNODES-1)/2];
int match2[MAXNODES*(MAXNODES-1)/2];
int index[MAXNODES][MAXNODES];
}user_problem;
The fields
match1,
match2, and
index will be used later in the code in order to map variables to the
corresponding assignment and vice versa.
Next, we need to read in the problem instance. We could implement this function within the user_io() callback function (see the file user_master.c). However, in order to show how it can be done explicitly, we will define our own function match_read_data() in user_main.c to fill in the user data structure and then use sym_set_user_data() to pass this structure to SYMPHONY. The template code already provides basic command-line options for the user. The “-F” flag is used to specify the location of a data file, from which we will read in the data. The datafile contains first the number of nodes in the graph ( nnodes) followed by the pairwise cost matrix (nnode by nnode). We read the file in with the match_read_data() routine in user_main.c:
int match_read_data(user_problem *prob, char *infile)
{
int i, j;
FILE *f = NULL;
if ((f = fopen(infile, "r")) == NULL){
printf("main(): user file %s can't be opened\n", infile);
return(ERROR__USER);
}
/* Read in the costs */
fscanf(f,"%d",&(prob->numnodes));
for (i = 0; i < prob->numnodes; i++)
for (j = 0; j < prob->numnodes; j++)
fscanf(f, "%d", &(prob->cost[i][j]));
return (FUNCTION_TERMINATED_NORMALLY);
}
We can now construct the integer program itself. This is done by specifying
the constraint matrix and the rim vectors in sparse format. We will have a
variable for each possible assignment
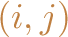with
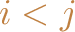. We have a constraint
for each node
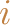, so it can only me matched to one other node.
We define the IP in our other helper function match_load_problem() in user_main.c. In the first part of this routine, we will build a description of the IP, and then in the second part, we will load this representation to SYMPHONY through sym_explicit_load_problem(). Note that we could instead create a description of each subproblem dynamically using the user_create_subproblem() callback (see user_lp.c), but this is more complicated and unnecessary here.
int match_load_problem(sym_environment *env, user_problem *prob){
int i, j, index, n, m, nz, *matbeg, *matind;
double *matval, *lb, *ub, *obj, *rhs, *rngval;
char *sense, *is_int;
/* set up the inital LP data */
n = prob->numnodes*(prob->numnodes-1)/2;
m = 2 * prob->numnodes;
nz = 2 * n;
/* Allocate the arrays */
matbeg = (int *) malloc((n + 1) * ISIZE);
matind = (int *) malloc((nz) * ISIZE);
matval = (double *) malloc((nz) * DSIZE);
obj = (double *) malloc(n * DSIZE);
lb = (double *) calloc(n, DSIZE);
ub = (double *) malloc(n * DSIZE);
rhs = (double *) malloc(m * DSIZE);
sense = (char *) malloc(m * CSIZE);
rngval = (double *) calloc(m, DSIZE);
is_int = (char *) malloc(n * CSIZE);
/* Fill out the appropriate data structures -- each column has
exactly two entries */
index = 0;
for (i = 0; i < prob->numnodes; i++) {
for (j = i+1; j < prob->numnodes; j++) {
prob->match1[index] = i; /*The first component of assignment 'index'*/
prob->match2[index] = j; /*The second component of assignment 'index'*/
/* So we can recover the index later */
prob->index[i][j] = prob->index[j][i] = index;
obj[index] = prob->cost[i][j]; /* Cost of assignment (i, j) */
is_int[index] = TRUE;
matbeg[index] = 2*index;
matval[2*index] = 1;
matval[2*index+1] = 1;
matind[2*index] = i;
matind[2*index+1] = j;
ub[index] = 1.0;
index++;
}
}
matbeg[n] = 2 * n;
/* set the initial right hand side */
for (i = 0; i < m; i++) {
rhs[i] = 1;
sense[i] = 'E';
}
/* Load the problem to SYMPHONY */
sym_explicit_load_problem(env, n, m, matbeg, matind, matval, lb, ub,
is_int, obj, 0, sense, rhs, rngval, true);
return (FUNCTION_TERMINATED_NORMALLY);
}
Now, we are ready to gather everything in the main() routine in user_main(). This will involve to create a SYMPHONY environment and a user data structure, read in the data, create the corresponding IP, load it to the environment and ask SYMPHONY to solve it ( CALL_FUNCTION is just a macro to take care of the return values):
int main(int argc, char **argv)
{
int termcode;
char * infile;
/* Create a SYMPHONY environment */
sym_environment *env = sym_open_environment();
/* Create the data structure for storing the problem instance.*/
user_problem *prob = (user_problem *)calloc(1, sizeof(user_problem));
CALL_FUNCTION( sym_set_user_data(env, (void *)prob) );
CALL_FUNCTION( sym_parse_command_line(env, argc, argv) );
CALL_FUNCTION( sym_get_str_param(env, "infile_name", &infile));
CALL_FUNCTION( match_read_data(prob, infile) );
CALL_FUNCTION( match_load_problem(env, prob) );
CALL_FUNCTION( sym_solve(env) );
CALL_FUNCTION( sym_close_environment(env) );
return(0);
}
OK, that's it. That defines an integer program, and if you compile and optimize it, the rest of the system will come together to solve this problem. Here is a data file to use:
6 0 1 1 3 3 3 1 0 1 3 3 3 1 1 0 3 3 3 3 3 3 0 1 1 3 3 3 1 0 1 3 3 3 1 1 0
The optimal value is 5. To display the solution, we need to be able to map back from variables to the nodes. That was the use of the node1 and node2 parts of the USER_PROBLEM. We can now use user_display_solution() in user_master.c to print out the solution:
int user_display_solution(void *user, double lpetol, int varnum, int *indices,
double *values, double objval)
{
/* This gives you access to the user data structure. */
user_problem *prob = (user_problem *) user;
int index;
for (index = 0; index < varnum; index++){
if (values[index] > lpetol) {
printf("%2d matched with %2d at cost %6d\n",
prob->node1[indices[index]],
prob->node2[indices[index]],
prob->cost[prob->node1[indices[index]]]
[prob->node2[indices[index]]]);
}
}
return(USER_SUCCESS);
}
We will now update the code to include a crude cut generator. Of course, We could go for a Gomory-Hu type odd-set separation (ala Grötschel and Padberg) but for the moment, let's just check for sets of size three with more than value 1 among them (such a set defines a cut that requires at least one edge out of any odd set). We can do this by brute force checking of triples, as follows:
int user_find_cuts(void *user, int varnum, int iter_num, int level,
int index, double objval, int *indices, double *values,
double ub, double etol, int *num_cuts, int *alloc_cuts,
cut_data ***cuts)
{
user_problem *prob = (user_problem *) user;
double edge_val[200][200]; /* Matrix of edge values */
int i, j, k, cutind[3];
double cutval[3];
int cutnum = 0;
/* Allocate the edge_val matrix to zero (we could also just calloc it) */
memset((char *)edge_val, 0, 200*200*ISIZE);
for (i = 0; i < varnum; i++) {
edge_val[prob->node1[indices[i]]][prob->node2[indices[i]]] = values[i];
}
for (i = 0; i < prob->nnodes; i++){
for (j = i+1; j < prob->nnodes; j++){
for (k = j+1; k < prob->nnodes; k++) {
if (edge_val[i][j]+edge_val[j][k]+edge_val[i][k] > 1.0 + etol) {
/* Found violated triangle cut */
/* Form the cut as a sparse vector */
cutind[0] = prob->index[i][j];
cutind[1] = prob->index[j][k];
cutind[2] = prob->index[i][k];
cutval[0] = cutval[1] = cutval[2] = 1.0;
cg_add_explicit_cut(3, cutind, cutval, 1.0, 0, 'L',
TRUE, num_cuts, alloc_cuts, cuts);
cutnum++;
}
}
}
}
return(USER_SUCCESS);
}
Note the call of cg_add_explicit_cut(), which tells SYMPHONY about any cuts found. If we now solve the matching problem on the sample data set, the number of nodes in the branch and bound tree should just be 1 (rather than 3 without cut generation).